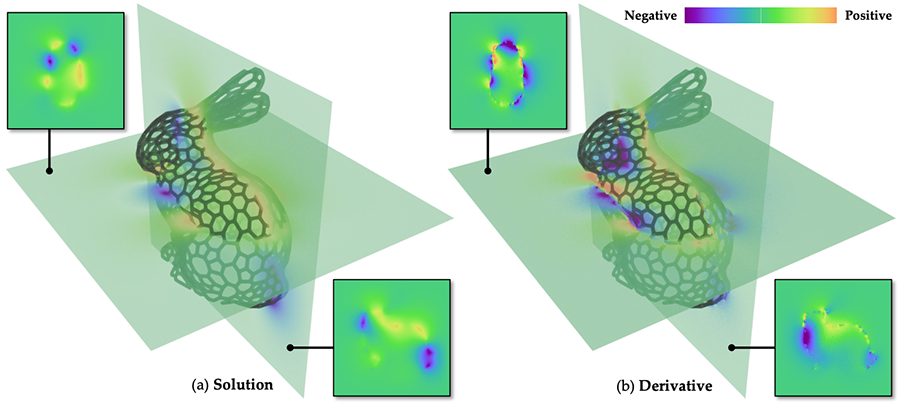
The Poisson equation is an important partial differential equation (PDE) with numerous applications in physics, engineering, and computer graphics. Conventional solutions to the Poisson equation require discretizing the domain or its boundary, which can be very expensive for domains with detailed geometries. To overcome this challenge, a family of grid-free Monte Carlo solutions has recently been developed. By utilizing walk-on-sphere (WoS) processes, these techniques are capable of efficiently solving the Poisson equation over complex domains.
In this paper, we introduce a general technique that differentiates solutions to the Poisson equation with Dirichlet boundary conditions. Specifically, we devise a new boundary-integral formulation for the derivatives with respect to arbitrary parameters including shapes of the domain. Further, we develop an efficient walk-on-spheres technique based on our new formulation---including a new approach to estimate normal derivatives of the solution field. We demonstrate the effectiveness of our technique over baseline methods using several synthetic examples.
@inproceedings{Yu:2024:Diff-WOS,
title={A Differential Monte Carlo Solver For the Poisson Equation},
author={Yu, Z. and Wu, L. and Zhou, Z. and Zhao, S.},
booktitle = {ACM SIGGRAPH 2024 Conference Proceedings},
year = {2024},
}
We thank the anonymous reviewers for their constructive suggestions. We are also grateful to Aaron Lefohn for his support. This work started when Zihan Yu was an intern at NVIDIA. Zihan Yu and Zhiqian Zhou's contributions while at the University of California, Irvine were partially supported by NSF grant 1900927.