Boundary integrals are unique to physics-based differentiable rendering and crucial for differentiating with respect to object geometry. Under the differential path integral framework—which has enabled the development of sophisticated differentiable rendering algorithms—the boundary components are themselves path integrals. Previously, although the mathematical formulation of boundary path integrals have been established, efficient estimation of these integrals remains challenging.

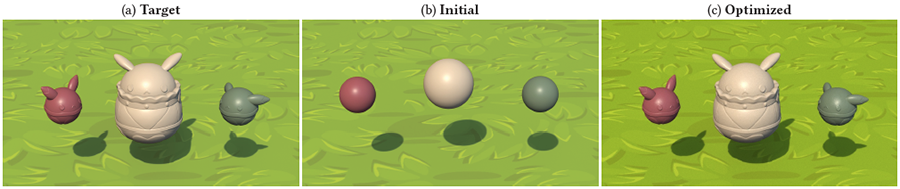
In this paper, we introduce a new technique to efficiently estimate boundary path integrals. A key component of our technique is a primary-sample-space guiding step for importance sampling of boundary segments. Additionally, we show multiple importance sampling can be used to combine multiple guided samplings. Lastly, we introduce an optional edge sorting step to further improve the runtime performance. We evaluate the effectiveness of our method using several differentiable-rendering and inverse-rendering examples and provide comparisons with existing methods for reconstruction as well as gradient quality.

• Paper: pdf (19 MB)
• Supplemental material: html, zip (205 MB)
• Code: Github

@article{Yan:2022:Guiding,
  title={Efficient Estimation of Boundary Integrals for Path-Space Differentiable Rendering},
  author={Yan, Kai and Lassner, Christoph and Budge, Brian and Dong, Zhao and Zhao, Shuang},
  journal={ACM Trans. Graph.},
  volume={41},
  number={4},
  year={2022},
  pages={123:1--123:13}
}

We thank the anonymous reviewers for their constructive comments and suggestions. Thanks to the Stanford University Computer Graphics Laboratory for the Bunny model. This work started when Kai Yan was an intern at Meta Reality Labs Research. Kai Yan's contributions while at the University of California, Irvine were partially supported by NSF grant 1900927.