CS114 Project 2:
Monte Carlo Integration & Path Tracing

Due: Wednesday May 6, 2020 (23:59 Pacific Time)

Part 1. Monte Carlo Integration

In this part, you will implement several Monte Carlo estimators for computing integrals and compare their efficiencies.

Please submit a ZIP package for this task containing:

Task 1. One-Dimensional Problems

Task 1-1. Warming up

Compute the following integral $$ I = \int_{-2}^2 \exp\left(-\frac{x^2}{2}\right)\,\mathrm{d}x, $$ (where $\exp()$ denotes the natural exponential function) using Monte Carlo integration with density function $$ p(x) \equiv \frac{1}{4} \quad\text{for all $-2 \leq x < 2$.} $$

You should start with drawing $N = 100\ 000$ samples $x_1,\ x_2,\ \ldots,\ x_N \in [-2, 2)$:

With $x_1,\ x_2,\ \ldots,\ x_N$ generated, you then need to evaluate $\hat{I}_{\!1},\ \hat{I}_{\!2},\ \ldots,\ \hat{I}_{\!N}$ given by: $$ \hat{I}_{\!j} = \frac{\exp(-x_j^2/2)}{p(x_j)} \quad\text{for $j = 1,\ 2,\ \ldots, N$}, $$ and include the following in your report:

Please execute your code 10 times (with non-fixed random seeds), and you should get 10 sets of slightly different $\bar{I}$ and $\bar{s}$ values. Report all of them (rounded to three decimal places) in a table that looks like:

Round $\bar{I}$ $\bar{s}$
1 x.xxx x.xxx
2 x.xxx x.xxx
$\vdots$ $\vdots$ $\vdots$
10 x.xxx x.xxx

Remark: If you implement everything correctly, the interval $[ \bar{I} - \bar{s},\ \bar{I} + \bar{s} ]$ should contain the correct answer 2.3926 about 95% of the time. As a result, this interval is called a 95% confidence interval.

Task 1-2. Integrals over Unbounded Intervals

Compute the following integral $$ I = \int_{1}^{\infty} \exp\left(-\frac{x^2}{2}\right)\,\mathrm{d}x. $$

Since this integral is defined over the unbounded interval $[1, \infty)$, uniform distributions cannot be used. Instead, please draw $\xi$ uniformly from $[0, 1)$, and set $$ x = 1 - \frac{\log \xi}{\lambda} $$ (where $\log()$ is the natural logarithm function) with some fixed $\lambda > 0$. In this case, $x$ will be distributed exponentially with probability density $$ p(x ; \lambda) = \lambda \exp(-\lambda (x - 1)). $$

Please try three different $\lambda$ values: 0.1, 1.0, and 10.0. For each $\lambda$, create a table with 10 sets of $\bar{I}$ and $\bar{s}$ values each of which uses $N = 100\ 000$ independent samples (similar to Task 1-1). Then, discuss in your report:

Task 2. Integrals over Unit Spheres

Task 2-1. Surface Area of the Hemisphere

As discussed in class, the surface area of a unit hemisphere can be computed using sphere coordinates ($\theta$, $\phi$) as $$ \int_0^{2\pi} \int_0^{\pi/2} \sin\theta \mathrm{d}\theta \mathrm{d}\phi. $$ Let $A := [0, \frac{\pi}{2}) \times [0, 2\pi)$ be a 2D rectangle, then the previous integral can be rewritten as $$ I := \int_A \sin({\bf x}[1])\,\mathrm{d}{\bf x}, $$ where ${\bf x}$ is a 2D vector and ${\bf x}[1]$ denotes its first component (that is, if ${\bf x} = (a, b)$, then ${\bf x}[1] = a$).

Use Monte Carlo integration to estimate $I$ by uniformly sampling ${\bf x}$ from $A$. That is, generating each sample by:

Include a table similar to Task 1-1 in your report.

Task 2-2. Arbitrary Spherical Function

Let $$ \begin{aligned} \theta &= \arccos(\xi_1),\\ \phi &= 2\pi\xi_2, \end{aligned} $$ where $\xi_1,\ \xi_2$ are drawn independently from $U[0, 1)$. Then it can be shown that $\omega := (\theta, \phi)$ in spherical coordinates is distributed uniformly over the hemisphere centered at (0, 0, 0). That is, $$ p(\omega) \equiv \frac{1}{2\pi}, $$ for all $\omega$'s generated this way.

Use this sampling scheme to estimate the following integral: $$ I = \int_{\Omega_+} (\cos\theta\,\sin\theta\,\cos\phi)^2\,\mathrm{d}\omega, $$ where $\Omega_+$ denotes the entire unit hemisphere with $\theta \in [0, \frac{\pi}{2})$. Include a table similar to Task 1-1 in your report.

Task 3. Estimating Radiant Flux

Consider a simple 3D scene with two objects:

This light source is a uniform emitter: its emitted radiance (at any point on the surface in any direction) is fixed to $L = 100$. Then, the radiant flux (i.e., power) received by $R$ equals $$ P = \int_R \int_{\Omega_+} L \cdot \chi({\bf x}, \omega) \cdot \cos\theta\,\mathrm{d}{\omega}\,\mathrm{d}{\bf x}, $$ where $\theta$ is the angle between $\omega$ and the Z-axis, and $\chi$ is an indicator function given by $$ \chi({\bf x}, \omega) = \begin{cases} 1 & \text{if ray $({\bf x}, \omega)$ hits $S$,}\\ 0 & \text{otherwise}. \end{cases} $$ Two examples are shown below:

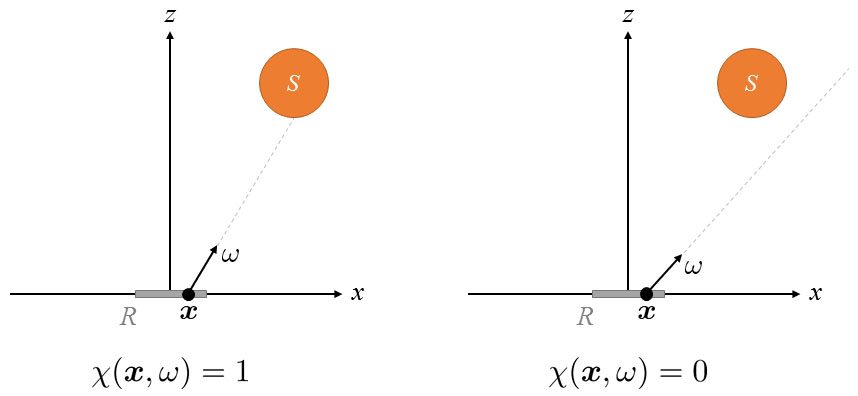
Use Monte Carlo integration to estimate $P$ by uniformly sampling ${\bf x} \in R$ and $\omega \in \Omega_+$. Pick proper number of samples so that the resulting estimation is accurate to one decimal place. Report your estimated $P$ value and the number of samples used.

Extra Credit: Use non-uniform sampling for $\omega$ to achieve better convergence rate. Describe in your report: